Structural Equation Models (SEMs)
You can think of Structural Equation Models (SEMs) as an extension of the General Linear Model that proves to be more versatile and more powerful than multiple regression analysis. One way to think of SEMs is as a hybrid between factor analysis and regression analysis. Given the power and diversity of application, you shouldn’t think of SEM in terms of a single statistical technique like a t-test or a correlation. It may be more helpful to think of it as a general modeling framework that can be customized to many different research questions. Rather than having a fixed structure, you can model many different structures depending on your research purpose.
SEMs have several known aliases:
-Causal modeling
-Latent variable models
-Models with unobserved variables
-Analysis of covariance structures
-Structural modeling
Because it is the most general method known to date, SEM is the most versatile analytical method available to researchers.
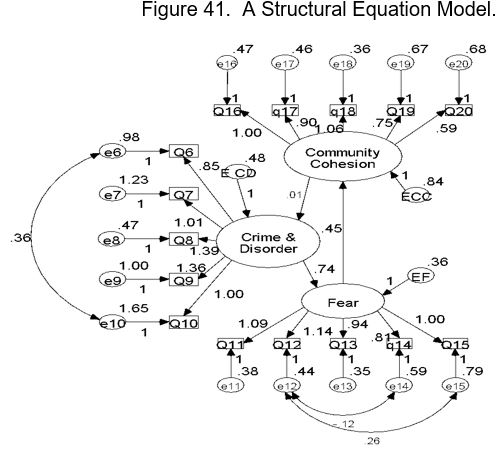
The above figure represents a structural equation model that depicts the relationships specified by the Broken Windows Theory. Note that the shapes represent different aspects of the model. The squares (rectangles) represent individual observed variables (survey responses). The ovals below each rectangle represent the error terms; in regression analysis, we pretend these don’t exist most of the time. In SEM, they are explicitly modeled. The ovals represent the latent constructs that the indicator variables measure. The arrows from the ovals to the squares signify that the latent construct causes each of the survey responses. The number that goes with each arrow represents the linear relationship between the measured variable and the latent construct. The arrows between the ovals represent the relationships between the latent constructs. In the example, it is hypothesized that fear of crime causes a breakdown in community cohesion (informal social controls) and that in turn causes an increase in crime and disorder. Note that the arrows form a causal loop, which represents the “spiral of decay” that Broken Windows Theory suggests. This sort of loop cannot be modeled in path analysis, making SEM superior in that regard.
In SEM convention, straight arrows represent causal relationships that are directional. Curved arrows represent correlations where no causal direction is specified. When error terms are correlated, this can be accounted for in the model, whereas with regression analysis we assume they are not correlated. In the model above, then, we can see that Fear is hypothesized to cause Community Cohesion. We can also see that Community Cohesion is hypothesized to cause Crime and Disorder. We can think of all of the squares connected to a single oval as a factor model, similar to what we would get if we did a factor analysis with all of the variables represented by the squares. In this study, we can see that that the model is composed of three factors, which are defined by the survey responses. We can think of the relationships specified between the latent variables (ovals) as separate regression models. This obviously allows us to model incredibly complex models with many different measurements related to the latent constructs.
Note that the graphical image presents the coefficients for each “path,” but there are tons of other numbers that usually don’t get printed in the journal article. SEMs produce a truly amazing amount of numbers and can be very difficult to interpret. Behind the scenes, the paths are specified by sets of equations. The hypothesized model under study can be tested statistically in a simultaneous analysis of the entire system of variables to determine the extent to which it is consistent with the data. The math was mind-blowing until the advent of the graphical interfaces we use today. The most popular of these is known as AMOS.
SEM a methodology that takes a confirmatory (hypothesis testing) approach to the analysis of a structural theory bearing on some phenomenon.
It can be viewed as a combination of factor analysis and regression analysis; if you don’t have a good understanding of those methods, you will not get SEMs. The most important aspect of SEM is its ability to model the effects of latent variables (factors) on each other.
Note that all we said in previous sections about causation still applies. Covariation is not causation. Theory is paramount in the development of structural equation models, and SEM is best at disconfirming theories. It can only support causal theories, not prove them. A particular model may be consistent with the data and get causation wrong. Recall that a model is a mathematical representation of the theoretical conception under study. Models represent the relationships between the variables that are hypothesized in theory.
Structural equations summarize mathematically the impact of all relevant variables in the model on a single variable. Thus the equation for a particular variable is the sum of all variables that have arrows pointing to it.
Last Modified: 02/14/2019
