Section 4.4: Linear Regression
When variables are correlated, we can use knowledge of one to predict the value of the other. That is, we can study the relationship between variables that are known, and use our knowledge of that relationship to predict future values when one of the variables is not known. For example, a university admissions office might use your SAT score to predict your success in college based on what they observed about the relationship between SAT scores and college success in past students. The statistical technique that allows us to derive an equation to make such predictions is known as regression.
In linear regression, a line is mathematically fitted to the dots on a scattergram. The idea of the line is to split the field of dots down the middle, much like the seam on a football.
By using a mathematical equation derived from the regression line, we can derive a regression equation that allows us to predict the value of an unknown score (y) using information from a known variable (x). A straight line can be represented mathematically by the following formula:
Where ![]() stands in for the value we want to predict, a is the intercept (the score where the regression line meets the vertical axis) and b is the slope of the line (the direction and angle of the line).
stands in for the value we want to predict, a is the intercept (the score where the regression line meets the vertical axis) and b is the slope of the line (the direction and angle of the line).
Thus to predict a score for Y given X, we first need to obtain values for a and b. In the case of multiple regression, this involves some very complex math and is best accomplished using a computer.
Let us say, for example, a statistics professor is curious as to whether scores on the first test are a valid predictor of scores on a final exam. He enters the scores into a spreadsheet and generates the scatterplot illustrated below. We can determine several things by examining this scatterplot. First, notice the line running through the dots. This is the regression line (also known as a trend line). The dots fall “pretty close” to the line, but they do not fall along it exactly. From this, we can tell that the correlation is a strong one, but it is not perfect.
Also, note that R2 is reported. This tells us that 83.88% of the variance in Y is explained by knowing X.
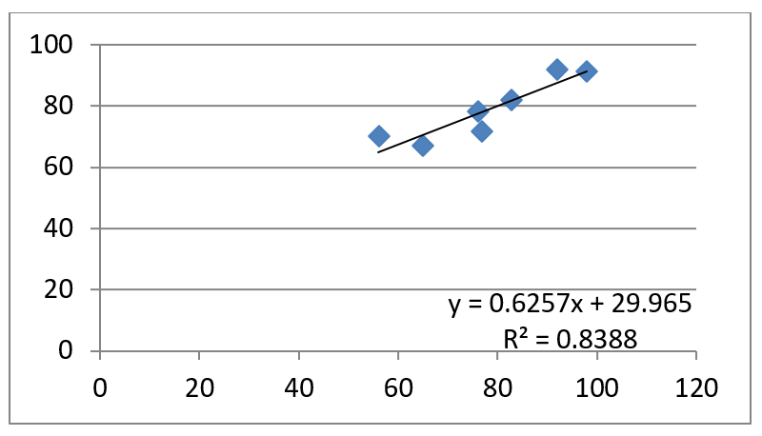
The regression equation is also reported as Y = 0.6257X + 29.965. With this equation, we can make future predictions about what Y will be for an individual given X. For example, let us say a student makes a score of 90 on the first exam. What is his final exam grade likely to be? We can easily determine this by multiplying 0.6257 by 90 to get 56.313. The product is then added to the constant of 29.965 to yield a predicted Y value of 86.278.
It is important to realize that linear regression is useful only if the dots form a straight line. If there is no line to speak of or the line must curve one or more times to adequately fit the data, then linear regression should not be used.
[ Back | Contents | Next ]
Last Modified: 010/10/2018[amazon_link asins=’1983091049′ template=’ProductCarousel’ store=’thereferencepage’ marketplace=’US’ link_id=’f6d2aba5-7e38-11e8-a89f-0f73c296ad50′]