Many of the statistical methods discussed in this book can be computed using Microsoft’s powerful and popular spreadsheet program Excel. The Data Analysis ToolPak is not installed with the standard Excel setup. Look in the Tools menu. If you do not have a Data Analysis item, you will need to install the Data Analysis tools. Search Help for “Data Analysis Tools” for instructions, or see the box below for a brief explanation.
The word data is actually the plural of datum; datum refers to a single value, while data refers to a collection of values.
To make statistical computations in Excel, you must first learn how to use functions. A function is a formula that is predefined within Excel to accomplish a specific task. Remember that in a table of numbers such as a spreadsheet, the lines of numbers going up and down are called columns, and the lines of numbers going side to side are called rows. Let us say we want to do something simple like compute the average for a quiz taken by our statistics class. We can set up an Excel sheet to do the job as follows:
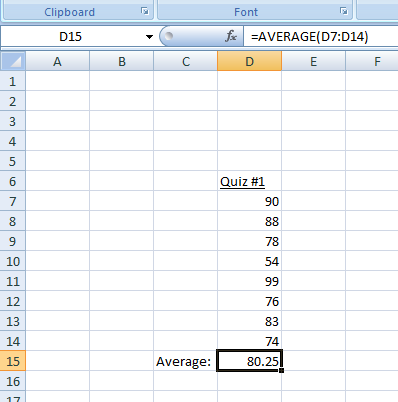
Note that all of the quiz scores are placed in a column. The value 80.25 is the average (mean). The value was not typed in, however. Excel put it there. What was typed in was the function. Functions may look a little complicated at first, but they are very easy to use once you understand the anatomy. In the function bar at the top of the table, we see the syntax =AVERAGE(D7:D14). All functions in Excel begin with an equal sign. That is how Excel knows it is a function and not just text or numbers. We could have placed the function in any cell, but it makes sense to put it at the end of the column. AVERAGE is the name of the predefined function that we are using to compute the mean. The (D7:D14) tells Excel to compute the average of the range of cells D7 through D14.
To insert a function automatically, first, click on the cell where you want to place the function. Then, under the formulas tab, click insert function. This will open the insert function dialog box. Most of the functions we will be using will be found under the “statistical” category.
Last Modified: 06/29/2018